0. Intro
TextRank는 텍스트 처리에 있어 그래프 기반의 랭킹 모델이며, 본 논문에서는 이를 이용하여 keyword extraction(키워드 추출)과 sentence extraction(핵심 문장 추출) 두가지 기능을 제공한다.
TextRank를 이해하려면 학습 기반이 되는 PageRank를, 그를 이해하기 위해서는 Markov Chain에 대해서 알아야 한다. 그러니 논문에 들어가기 앞서 알아야 하는 내용부터 다루도록 한다.
1. Markov Chain
마르코프 연쇄(Markov Chain)는 마르코프 성질을 가진 이산 확률과정이다. 이 때 마르코프 성질은 마치 사슬처럼 ‘특정 상태의 확률은 오직 과거의 상태에 의존한다’는 것이다. 예를 들면 오늘 맑으면 간단하게 내일 날씨가 맑을지 흐릴지 확률적으로 표현할 수 있다(실제 날씨는 훨씬 복잡하게 확률을 구하겠지만 간단하게 보자면 그렇다는 거).
예를 들어, 집과 학교가 있다. 집에서 학교로 갈 확률은 0.3, 학교에서 집으로 갈 확률은 0.8이고 장소는 집과 학교 둘 뿐이다. 매일 집과 학교 둘 중 한 군데로 갈 수 밖에 없다면, 확률로 나타내자면 다음과 같다. (추이행렬)
\[\begin{bmatrix} 0.7 & 0.8 \\ 0.3 & 0.2 \end{bmatrix}\begin{bmatrix} 집 \\ 학교 \end{bmatrix} = \begin{bmatrix} 0.7집 + 0.8학교 \\ 0.3집 + 0.2학교 \end{bmatrix}\]여기서 0.7은 집에서 집으로 가는 확률, 0.8은 학교에서 집으로 가는 확률을 나타낸다. 만약 이 확률이 계속된다면 다음 날에도 이렇게 되겠지.
\[\begin{bmatrix} 0.7 & 0.8 \\ 0.3 & 0.2 \end{bmatrix}\begin{bmatrix}0.7집 + 0.8학교 \\ 0.3집 + 0.2학교 \end{bmatrix} = \begin{bmatrix}0.73집+0.72학교\\ 0.27집 + 0.28학교\end{bmatrix}\]n일이 지났을 때는 결과적으로 아래와 같은 값이 나온다. 이 때 추이행렬의 무한제곱은 결국 하나의 극한 행렬에 수렴하게 되며 결국 집과 학교에 있는 사람들이 더 이상 이동하지 않고 안정적인 상태에 이르게 되었을 때의 인구 분포를 알 수 있다.
\[\begin{bmatrix} 0.7 & 0.8 \\ 0.3 & 0.2 \end{bmatrix}^n\begin{bmatrix} 집 \\ 학교 \end{bmatrix}\]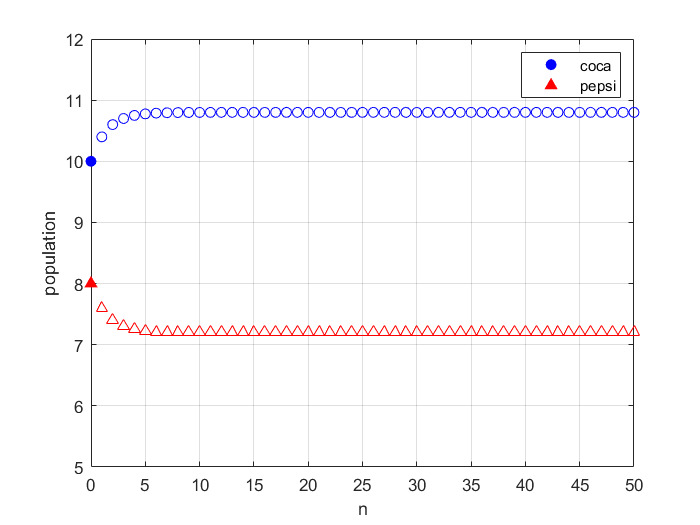
마르코프 연쇄 예시 그래프
2. PageRank
PageRank는 대표적인 Graph ranking 알고리즘으로 초기 구글에서 검색 결과값으로 나오는 웹페이지들의 ranking을 구하는 데 사용됐다. Page Rank에 사용된 아이디어는 굉장히 직관적이다. 일종의 ‘투표’라고 생각하면 이해하기 쉽다. 다른 웹페이지들(backlinks)로부터 투표를 많이 받은 페이지는 점수가 크며, 점수가 클수록 중요한 페이지라고 볼 수 있다. 하지만 모든 페이지가 같은 점수를 가지고 있지는 않으므로 투표를 적게 받더라도 중요한 페이지로부터 투표를 받으면 점수가 높아질 수 있다.
PageRank에서 각 페이지의 중요도 $PR(u)$는 다음과 같이 계산된다. 이 때 $B_u$는 페이지 $u$의 backlinks로 $v$에서 $u$로 가는 링크가 있다고 생각하면 된다. 각 페이지 $v$는 자신이 가진 link의 개수($N_v)$만큼 나눠서 각각의 page $u$에 전달한다.
\[PR(u) = c \times \sum_{v \in B_u} \frac{PR(v)}{N_v} + (1 - c) \times \frac{1}{N}\]왜 자신이 가진 link의 개수만큼 나눌까? $\sum_{v \in B_u} \frac{PR(v)}{N_v}$ 이 부분을 자세히 설명하자면 다음과 같다. 예를 들어 ranking 100의 페이지가 두 개의 페이지에 대해 backlinks로 존재한다면 두 개의 페이지에 각각 50점씩 들어간다. 이걸 개미의 이동 모델로 설명하기도 한다는데, N개의 마디가 존재하는 그래프에 각 마디마다 공평하게 $\frac {1}{N}$마리의 개미가 간다고 생각하면 쉽다. Backlinks가 많은 페이지는 많은 개미가 모인다. 이 과정은 한 번이 아니라 여러 번 수행한다.
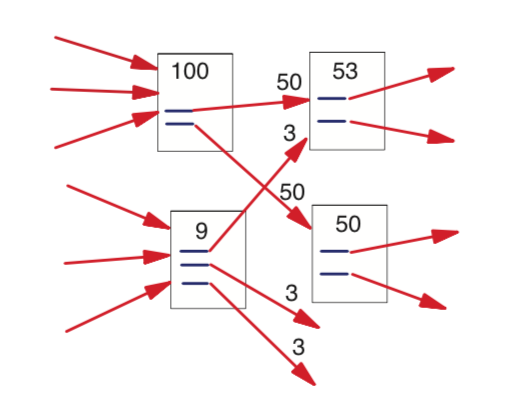
이런 과정을 확률 분야에서는 Markov Model이라고 부르며 개미가 이동하는 비율이 마르코프 체인의 추이행렬에 해당한다. 아래에 예시로 설명한다.
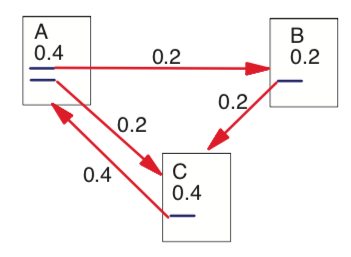
위 그림의 이동을 행렬로 간단하게 0과 1로 표현하면 다음과 같다.
\[\begin{bmatrix} 0 & 0 & 1 \\ 1 & 0 & 0\\1&1&0 \end{bmatrix}\]이제 edge를 따라 개미가 몇 마리 가는지를 추이행렬로 바꾸면 다음과 같다.
\[\begin{bmatrix} 0 & 0 & 1 \\ \frac{1}{2} & 0 & 0\\\frac{1}{2}&1&0 \end{bmatrix} \begin{bmatrix} A\\B\\C\end{bmatrix} = \begin{bmatrix}C\\\frac{1}{2}A\\\frac{1}{2}A+B\end{bmatrix}\]이 과정이 여러 번 반복된다고 하니, 마르코프 체인에서 봤듯이 해당 행렬을 무한히 제곱하면 A, B, C 페이지의 안정적인 점수가 나오며 그 점수가 PageRank인 것이다.
그럼 $c$라는 상수는 왜 곱하느냐.. 우선 PageRank는 그래프가 cyclic 해야지만 제대로 계산이 된다. 하지만 어떤 페이지는 backlinks만 있고 다른 페이지로 연결되는 링크가 없을 수도 있다(dangling node). 이 경우에는 개미가 들어가기만 할 뿐 나가지 못하는데 그럼 해당 페이지의 점수를 보낼 곳이 없어진다. 이를 해결하기 위해서 각 페이지에 존재하는 개미의 $c$만큼 남겨둔다. 이 때 $c$는 보통 0.85로 정한다. $(1-c)$만큼의 개미는 임의의 노드로 보내며, 다른 마디로 나눠서 가기 때문에 $\frac{(1-c)}{N}$로 계산된다. 즉 $c$는 링크에 의한 유입, $(1-c)$는 임의 유입이라고 생각하면 된다. 이렇게 하면 모든 마디가 연결되어 cyclic network가 된다.
3. TextRank
이제 TextRank에 대해서 알아보자. 본 논문은 2가지 NLP 태스크를 수행한다; 키워드 추출 그리고 문장 추출. 이 때 태스크는 두 개의 연속된 노드 결과값의 차이가 threshold 미만으로 떨어질 때 값이 수렴하며 그 때 계산을 마친다는 점을 알아두자.
TextRank는 텍스트 단위의 local context(어휘 단위; 정점)만 염두에 두는 게 아니라 전체 텍스트에서 반복적으로 정보를 뽑아왔다는 점(어휘 간의 관계; 간선)에서 의미가 있다. 그리고 한 텍스트 단위가 관련된 다른 텍스트 단위를 추천해준다는 점에서도 특징이 두드러진다. 키워드 추출에서는 동시에 나타나는 단어들이 서로를 중요하다고 “추천”해주며, 문장 추출에서는 비슷한 내용을 담은 문장들이 서로를 “추천”해준다.
Keyword Extraction
키워드 추출은 document를 가장 잘 설명하는 문자를 추출하는 일이다. 본 논문에서는 Abstract 데이터에서 키워드 추출을 진행하였다. 그래프는 undirected이며 정점과 간선은 다음과 같이 구성된다. 간선 같은 경우에는 co-occurrence relation을 사용하였다. 이는 단어 의미 판별(word sense disambiguation) 문제를 해소하기 좋기 때문이다.
- Vertex: 특정 pos 태그를 가진 1 개 또는 여러 개의 어휘.
- Edge: 두 어휘 사이의 관계를 정의할 수 있는 관계
키워드 추출 과정은 다음과 같다.
- 텍스트를 tokenize한 후, pos 태그화한다. (single words만)
- 수렴할 때까지 window size N의 단어 간 co-occurrence를 구한다.
- 후처리를 위한 상위 T개의 정점을 역순으로 정렬해서 구한다. (T = 1/3 vertices)
- 만약 상위 T개의 단어 중 일부가 문장 내에서 연속해서 나타난다면 multi-word 키워드로 합쳐진다. (e.g. Matlab code for plotting ambiguity functions; Matlab code가 하나의 단어로 처리)
키워드 추출을 진행한 결과를 분석하자면 다음과 같다.
- window size가 작을수록 성능이 더 좋다. 이는 멀리 떨어져 있는 단어들은 텍스트 내에서 서로의 상호 관계가 약하기 때문이다.
- pos 태그를 한 경우 결과가 좋게 나온다. 이는 언어적 정보가 키워드 추출을 돕는다는 이전 연구와 일맥상통한다.
- Directed graph(텍스트의 자연스러운 흐름으로 방향을 결정)은 성능이 좋지 않았다. Co-occurring 단어들에 있어서 자연스러운 ‘방향’이 없다는 걸 의미한다.
Sentence Extraction
문장 추출은 extractive summary로 쓰인다. 이것 역시 비지도 학습이므로 문서 자동 요약에 쓰인다. 이 때 쓰이는 그래프에서 간선은 문장 간의 similarity relation을 사용했는데 이는 문장 간 내용이 얼마나 중복되는지로 구할 수 있다. 일종의 “추천”같은 게 A 문장은 독자에게 B 문장을 읽도록 “추천”해줄 수 있는데 그건 A와 B 문장 사이에 관계가 있기 때문이다. 이 때 문장 간 유사도는 다음과 같이 구한다. 두 문장에 공통으로 등장한 단어를 각 문장의 log 값의 합으로 나눈다.
\[sim(s_1, s_2) = \frac{\vert \{ w_k \vert w_k \in S_1 \& w_k \in S_2 \} \vert}{log \vert S_1 \vert + log \vert S_2 \vert}\]보통 문장 길이를 정규화해 유사도를 구하기 위해서 cosine similarity를 사용하지만 이는 짧은 문장에 민감하게 반응할 수 있다. 그래서 이 논문에서는 문장 간 유사도 구하는 공식을 새로 정의하였다. 길이가 긴 문장을 선호하는 걸 방지하기 위해 문장 길이의 log값을 합친 것을 분모로 사용하였지만 계산해보면 문장의 길이가 길수록 높은 유사도를 가진다. log값을 부여하면서 문장이 길어질수록 분모의 값은 작아지는데 겹치는 단어 수가 많으면 분자는 여전히 크기 때문에 유사도가 커진다. 즉, 의도와 달리 TextRank 는 길이가 긴 문장을 선호한다.
아무튼, 문장 추출에서는 한 문장이 다른 문장을 얼마나 추천해주는지가 중요하기 때문에 weighted graph를 사용한다. Weighted graph는 기존의 공식에서 가중치 값만 추가해주며 수식은 아래와 같다.
\[WS(V_i) = (1-d) + d \times \sum_{j \in In(V_i)} \frac{w_{ji}}{\sum_{V_k \in Out(V_j)} w_{jk}}WS(V_j)\]TextRank를 사용해서 Document Understanding Evaluations 2002 (DUC, 2002)에 사용된 신문 기사 데이터를 요약한다. 모델 성능 평가는 ROUGE를 사용하며, 직접 만든 요약본 2개로 평가한다. 결과는 sota가 아니지만 다른 시스템들은 학습된 반면, TextRank는 fully unsupervised 라는 점에서 높이 산다.
Reference
Markov Chain
PageRank
TextRank