1. Intro
저희는 이번 4월 한 달 동안 토픽 모델링(Topic Modeling)에 대해 배울 예정입니다. 그 시작으로 우선 잠재 의미 분석(Latent Semantic Analysis, 이하 LSA)을 다뤄보겠습니다. LSA는 토픽 모델링의 알고리즘과 직접적인 연관성을 지니고 있다고 보기 어렵습니다. 하지만 LSA는 새로운 의미공간(Semantic Space)을 창출하고 차원을 축소하는 데 ‘문헌-단어 행렬’을 활용했다는 점에서 토픽 모델링을 위한 아이디어를 직간접적으로 제공했다고 볼 수 있습니다.
Bag of Words 가정에서 출발한 문헌-단어 행렬 또는 TF-IDF는 기본적으로 단어의 빈도수를 이용해 단어의 의미를 찾고자 합니다. 논문에서도 기존 방식으로는 synonymy(동의어)와 polysemy(다의어)를 적절하게 인덱싱할 수 없음을 지적합니다. 동의어들이 많은 경우 information retrieval 과정에서 recall performance를 떨어뜨리고, 다의어가 많은 경우 precision performance를 저하시키는 것으로 알려져 있습니다. 즉 동의어 관계에 있는 두 단어의 의미적 유사성을 반영하거나, 문맥에 따라 각기 다른 의미를 갖는 다의어를 적절히 인덱싱하기 위해서는 문헌-단어 행렬의 카운트 기반 접근으로는 한계가 있는 것입니다.
LSA는 임베딩 방식에 비해서는 다소 고전적인 느낌이 있습니다. 하지만 LSA를 활용한 모델의 해석 가능성과 연산의 용이성으로 인해 여전히 현업에서 자주 사용되는 방식입니다. 특히 차원이 굉장히 큰 텍스트 데이터에 적용할 때 큰 효과를 볼 수 있는 것으로 알려져 있습니다.
2. Dimentionality Reduction(차원 축소)
차원 축소(Dimentionality Reduction)란 차원의 저주(Curse of Dimensionality)를 피하기 위해 사용할 수 있습니다. Features의 수가 굉장히 많은 데이터의 경우 과적합의 문제, 군집화 성능 저하 등 다양한 문제를 야기할 수 있습니다. 특히 텍스트 데이터의 경우 대개 하나의 문헌(document)이 수많은 단어(words)로 이루어져, 문헌의 수보다 단어의 수가 더 많은 경우가 왕왕 있습니다. 이렇듯 차원이 커지는 문제 외에도 대부분의 단어 features들이 0의 값을 지니기 때문에 sparse하다는 문제도 존재합니다. 전처리 과정에서 불용어 제거, 어근 추출 등을 시행한 이후에는 문헌 집합 내 존재하는 수많은 단어들 중 일부만이 task에 필요합니다.
이러한 문헌-단어 행렬에 대한 차원 축소를 시행할 경우 기대되는 효과는 크게 두 가지가 있습니다. 첫째로는 sparse matrix를 dense하게 만듦으로써 연산 효율성(computational efficiency)을 달성할 수 있습니다. 두번째로 분석/예측 task의 quality를 높일 수 있습니다. 텍스트 분류/군집화의 경우 차원 축소 과정에서 기존 데이터에 존재하는 noise를 제거함으로써 그 성능이 좋아진다고 알려져 있습니다.
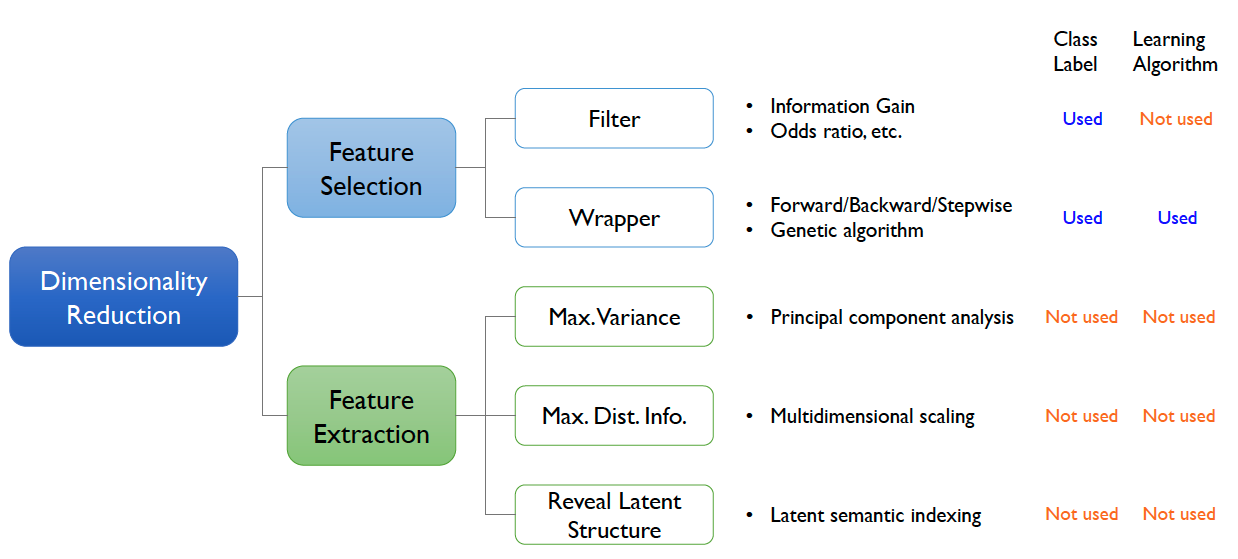
차원 축소에는 크게 두 가지 방법론이 있습니다. Feature selection(변수 선택)과 feature extraction(변수 추출)이 그 두 가지 방식입니다. 변수 선택을 통한 차원 축소는 데이터에 존재하는 features의 부분집합을 선택하는 방식입니다. 즉 변수의 개수가 줄지만 변수명 그 자체는 변화하지 않습니다. 반면 변수 추출의 경우 기존 변수들을 선형적으로 적절히 조합해서 새로운 변수를 생성하는 과정입니다.
변수 추출의 방식 중 하나인 PCA는 데이터의 분산을 최대로 보존하면서 서로 직교하는 새로운 기저를 찾아, 고차원 공간의 표본들을 저차원 공간으로 변환하는 기법입니다. 변수 추출의 또 다른 방식으로는 제가 이번에 다룰 Latent Semantic Indexing(=LSA)가 있습니다. LSI는 행렬의 선형변환에 의거한 행렬 분해 기법인 고유값 분해(Singular Value Decomposition, 이하 SVD)을 통해 행렬에 잠재적(latent)으로 존재하는 의미적 구조를 도출합니다. 즉 LSA를 이해하기 위해서는 SVD를 이해하는 과정이 반드시 필요합니다.
3. Singular Value Decomposition(특이값 분해)
특이값 분해는 가로 \(m\), 세로 \(n\) 크기의 행렬을 다음과 같이 분해(decomposition)하는 것을 뜻합니다. \(A=UΣV^\text{T}\) 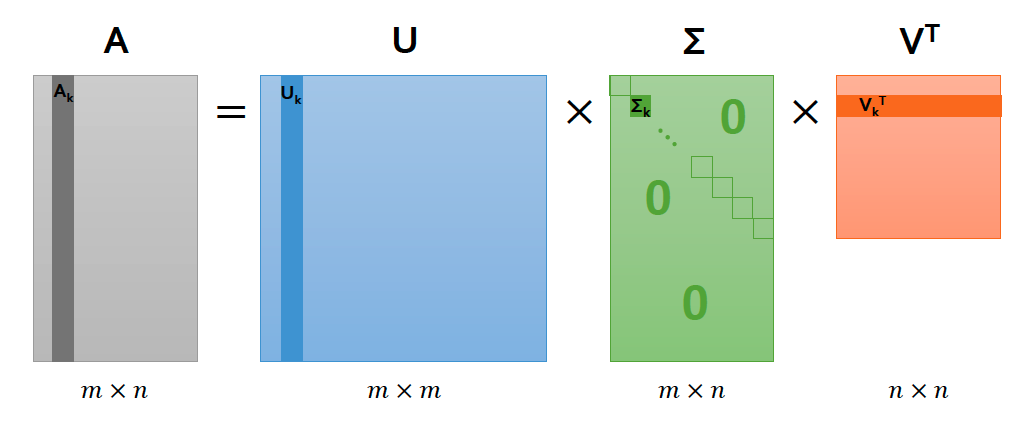
여기서 각 3개의 행렬은 다음과 같은 조건을 만족합니다. \(U: m × m\ \text{직교행렬}\ (AA^\text{T}=U(ΣΣ^\text{T})U^\text{T})\)
\[V: n × n\ \text{직교행렬}\ (A^\text{T}A=V(Σ^\text{T}Σ)V^\text{T})\] \[Σ: m × n\ \text{직사각 대각행렬}\]\(U\)는 \(AA^T\) 를 고유값분해(Eigenvalue Decomposition)해서 얻은 직교행렬로, \(U\)의 column vectors를 A의 left singular vector라고 부릅니다. \(V\)는 \(A^TA\)를 고유값분해해서 얻은 직교행렬로, \(V\)의 column vectors를 A의 right singular vector라 부릅니다. Σ는 \(AA^T, A^TA\)를 고유값분해해서 나오는 고유값들의 square root를 대각원소로 하는 가로 m, 세로 n 대각행렬입니다. 그때 해당 대각행렬의 대각원소를 \(A\)의 특이값(singular value)라고 부릅니다.
우선 해당 페이지에서는 특이값 분해의 선형대수학적 도출 과정보다는 의미적 해석에 초점을 두겠습니다(도출 과정은 세미나 중 설명드리겠습니다. 미리 훑어보고 싶은 분은 https://bskyvision.com/251 를 참고해주세요).
직교행렬 \(U\)와 직교행렬 \(V\)에 속한 열벡터(column vector)는 특이벡터(singluar vector)로 불리며, 다음의 성질을 지닙니다. $$ { \overrightarrow { { u }{ k } } }^{ T }\overrightarrow { { u }{ k } } =1,\quad { \overrightarrow { { v }{ k } } }^{ T }\overrightarrow { { v }{ k } } =1 \
{ \overrightarrow { { u }{ i } } }^{ T }\overrightarrow { { u }{ j } } =0,\quad { \overrightarrow { { v }{ i } } }^{ T }\overrightarrow { { v }{ j } } =1 \quad (i \not = j) \
{ U }^{ T }U=I,\quad{ V }^{ T }V=I \(즉 각각의 열벡터는 unit vector이며,\)U\(와\)V\(로 주어진 각 행렬 안에서 서로 다른 열벡터는 orthogonal한 관계를 지닙니다. 행렬\)Σ$$ 는 대각행렬로, 각 대각값이 고유값으로 구성되어있으며 큰 값부터 내림차순으로 정렬되어 있습니다. 각 특이값은 고유벡터와 고유값의 관계와 마찬가지로 대응되는 기저 벡터가 가지는 증감 정도, 즉 벡터에 미치는 scaling 정도를 의미합니다.
고유값분해와 비교해봤을 때, 고유값분해는 정방행렬에 대해서만 적용 가능합니다. 그리고 그 중에서도 일부 행렬에 대해서만 적용 가능한 대각화 방법입니다. 반면 특이값분해는 직사각행렬에도 적용 가능합니다. 그리고 전치행렬과의 곱(\(A^TA, AA^T\))을 사용한 대칭행렬을 사용하기 때문에 실수를 원소로 갖는 모든 직사각 행렬에 적용 가능합니다. 이러한 범용성 덕분에 SVD는 자연어, 비전, 추천시스템 등 다양한 분야에서 유용하게 사용되고 있습니다.
특이값분해의 3가지 축소(reduction) 방식
Thin SVD
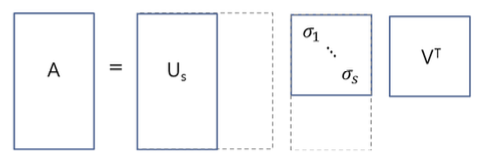
Thin SVD는 Σ 행렬의 아랫부분(비대각 파트 = 모두 0)을 제거하는 방식입니다. \(U\) 역시 Σ 차원에 맞춰서 열의 개수를 줄여줍니다. \(U\) 에서 제거된 부분은 본래 Σ 행렬의 0과 곱해지던 부분이기 때문에, 원래 결과에 영향을 주지 않습니다.
Compact SVD
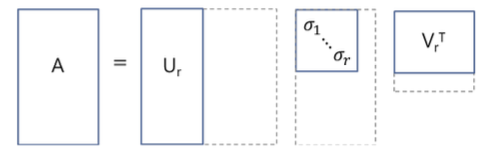
Σ 행렬에서 비대각파트 뿐만 아니라 대각원소(특이값)가 0인 부분도 제거하는 방식입니다. Compact SVD로도 원래 행렬 \(A\) 로 복원할 수 있습니다.
Truncated SVD
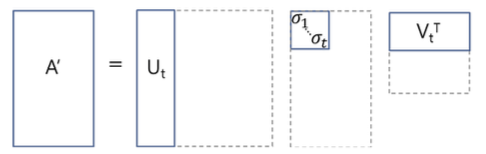
Σ 행렬의 대각원소(특이값) 가운데 상위 t개만 골라낸 형태입니다. 0이 아닌 특이값을 제외했기 때문에, 행렬 \(A\)를 완전히 원 상태로 복원하는 것은 불가능합니다. 하지만 t를 작은 숫자로 만들어서 데이터 정보를 엄청나게 압축했음에도 행렬 A의 원래 값에 근사하는 결과를 얻을 수 있습니다. 실제로 LSA는 이 방식을 사용해서 데이터를 압축하고 단어-문헌 행렬에서 잠재의미를 도출합니다.
4. Latent Semantic Indexing using SVD
기존 Indexing 방식의 문제점

해당 논문에서는 term-based information retrieval systems의 문제를 지적하기 위해 그림 6을 사용합니다. ‘IDF in computer-based information look-up’이라는 검색어를 입력했다고 가정해봅시다. 사용자는 쿼리와 관련이 있다고 판단한 문서에 대해, REL 열에 ‘R’로 표시를 합니다. 검색어(query)와 문서에 모두 등장하는 단어(여기서는 computer와 information)에 대해서는 해당 셀에 asterisk(*)로 표시되며, ‘MATCH’열에 ‘M’으로 표시된 문서는 시스템에 의해 사용자가 찾는 정보로 인식되어 return되었다는 것을 의미합니다.
여기서 문서 1과 문서 2가 당시 indexing 방식이 지닌 문제를 드러냅니다. 문서 1은 사용자가 검색하는 정보와 유사한 문서지만, 질의(query) 내 키워드를 포함하지 않기 때문에 관련 문서로 잡히지 않습니다. 반면 문서 2는 관련이 없는 문서지만 쿼리 내 단어들을 문서에 포함하기 때문에 사용자에게 관련 문서로 검색됩니다. 이를 일반화해서 생각해보면, Term-based information system은 동의어 간 유사성을 판별해내기 어렵고, 맥락에 따른 다의어의 의미 구분 역시 수행하기 어렵습니다. 이러한 문제점을 해결하기 위해서 연구에서는 implicit higher-order(latent) structure를 사용하고자 합니다.
SVD를 활용한 잠재의미분석
특이값분해를 활용한 문서, 단어의 잠재의미를 분석하는 과정 역시 단어-문헌 행렬(Term-Document matrix)에서 출발합니다. 해당 논문의 저자는 주어진 단어-문헌 행렬을 50-100개의 orthogonal factor를 사용해서 근사합니다(Truncated SVD). 50-100개로 추출된 각각의 차원은 단어와 문서의 common meaning component를 의미합니다. 즉 단어나 쿼리, 문헌의 ‘의미’가 k개의 값으로 표현될 수 있는 것입니다. 이러한 표현 방식은 각 단어와 문서를 \(k\)-space 안의 벡터로 표현할 수 있을 뿐만 아니라 기존의 N차원보다 훨씬 적은 k차원으로 의미를 표현할 수 있기에 dense matrix를 구축할 수 있습니다.
이렇듯 단어와 문헌은 잠재의미분석에서 각각 벡터로 표현될 수 있습니다. 사용자의 질의(query)는 단어들의 조합으로 구성됩니다. 질의에 포함된 각 단어들의 벡터를 가중합(weighted sum)해서 하나의 벡터로 표현할 수 있습니다. 이렇게 표현된 벡터와, 각 문서들의 벡터를 비교해 코사인 유사도가 가장 높은 n개의 문서를 검색 결과로 반환할 수 있는 것입니다.
특이값분해로 단어-문헌 행렬이 어떻게 잠재의미 벡터를 갖게 되는지를 구체적으로 살펴보겠습니다. 다음은 논문의 예시입니다.
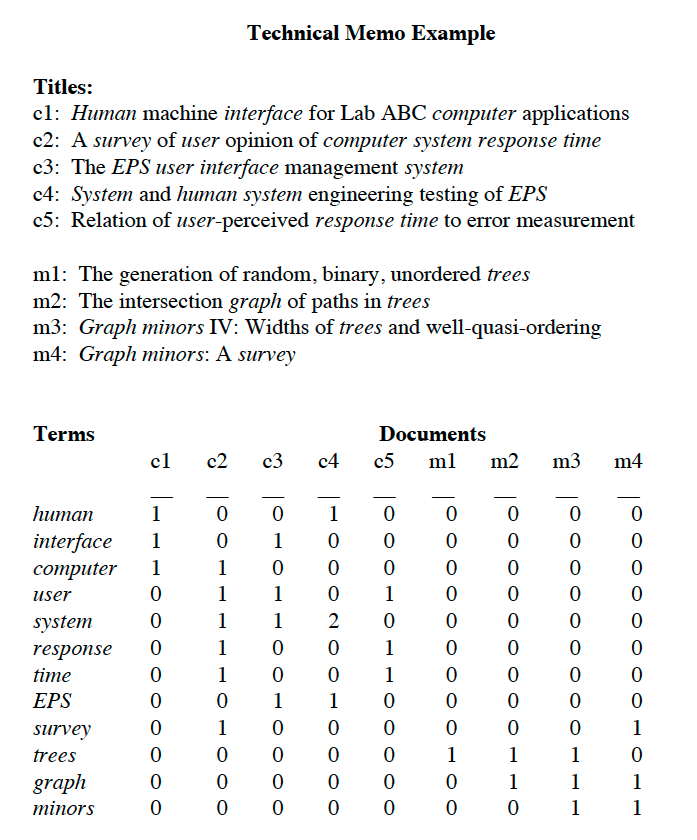

해당 예시의 데이터셋은 9개의 문헌과 12개의 단어로 구성되어 있습니다. 행렬을 특이값분해하면 다음과 같은 형태를 갖게 됩니다. \(X = T_0S_0D_0' \\\) \(T_0\) 와 \(D_0'\) 는 orthonormal columns로 구성되며, \(S_0\) 는 대각행렬입니다. 이에 대해 고유값 2개만을 사용해 2차원의 의미역을 구성하기 위한 truncated SVD를 진행한 결과는 다음과 같습니다.

그림 9를 보면 단어와 문헌이 모두 2차원의 vector로 표현됨을 확인했습니다. 이렇게 각 단어와 문헌을 \(k\) 차원 내의 벡터로 표현했을 때, 단순히 count 기반의 행렬을 사용했을 때보다 단어-단어, 문헌-문헌 사이 유사도를 잠재 의미를 고려해 파악할 수 있는 것입니다.
5. Conclusion
수많은 단어들로 이루어진 많은 문서들에 대한 검색을 진행할 때, 상위 \(k\) 개의 고유값을 사용한 SVD 방법론은 연산적 효율성을 보장해줍니다. 이러한 LSI 방법론은 기존의 방식이 동의어를 처리하는 방식에 비해서 훨씬 발전된 수준의 검색 결과를 제공합니다. 다만 다의어 문제에 대해서는 여전히 약점을 보입니다. 다의어는 character 적으로 하나의 고정된 형태만을 지니기 때문에, 맥락에 따라 다른 의미를 지닌 다의어라 하더라도 잠재 의미 공간 상에서는 결국 하나의 벡터로 표현되기 때문입니다.
Reference
- https://bskyvision.com/251
- https://ratsgo.github.io/from%20frequency%20to%20semantics/2017/04/06/pcasvdlsa/
- https://darkpgmr.tistory.com/106
- YouTube - KoreaUniv DSBA(https://www.youtube.com/channel/UCPq01cgCcEwhXl7BvcwIQyg)